
Combinaciones y permutaciones
¿Cuál es la diferencia?
En inglés usamos la palabra “combinación” sin pensar, sin pensar si el orden de las cosas es importante. En otras palabras:
“Mi ensalada de frutas es una combinación de manzanas, uvas y plátanos” No nos importa en qué orden están las frutas, también podrían ser “plátanos, uvas y manzanas “o” uvas, manzanas y plátanos “, es la misma ensalada de frutas.
“La combinación de la caja fuerte es 472” . Ahora a nos importa el pedido. “724” no funcionará, ni “247”. Tiene que ser exactamente 4-7-2 .
Entonces, en Matemáticas usamos un lenguaje más preciso :
- Cuando el orden no importa, es una Combinación .
- Cuando el orden importa es una Permutación .
|
¡Entonces, realmente deberíamos llamar a esto un “bloqueo de permutación”! |
En otras palabras:
Una permutación es una combinación ordenada .
| |
Para ayudarte a recordar, piensa “ P ermutación … P osition” |
Permutaciones
Básicamente hay dos tipos de permutación:
- Se permite la repetición : como el bloqueo de arriba. Podría ser “333”.
- Sin repetición : por ejemplo, las primeras tres personas en una carrera de carrera. No puedes ser el primero y segundo.
1. Permutaciones con repetición
Estos son los más fáciles de calcular.
Cuando una cosa tiene n diferentes tipos … ¡tenemos n opciones cada vez!
Por ejemplo: elegir 3 de esas cosas, las permutaciones son:
n × n × n
(n multiplicado 3 veces)
Más generalmente: eligiendo r de algo que tiene n diferentes tipos, las permutaciones son:
n × n × … (r veces)
(En otras palabras, hay n posibilidades para la primera opción, ENTONCES hay n posibilidades para la segunda opción, y así sucesivamente, multiplicándose cada vez.) [19459008 ]
Que es más fácil de escribir usando un exponente de r :
n × n × … (r veces) = n r
Ejemplo: en la cerradura de arriba, hay 10 números para elegir (0,1,2,3,4,5,6,7,8,9) y elegimos 3 de ellos:
10 × 10 × … (3 veces) = 10 3 = 1,000 permutaciones
Entonces, la fórmula es simplemente:
| n r |
| donde n es la cantidad de cosas para elegir, y elegimos r de ellos, se permite la repetición, y el orden importa. |
2. Permutaciones sin repetición
En este caso, tenemos que reducir el número de opciones disponibles cada vez.

Ejemplo: ¿en qué orden podrían estar 16 bolas de billar?
Después de elegir, por ejemplo, el número “14”, no podemos volver a elegirlo.
Entonces, nuestra primera opción tiene 16 posibilidades, y nuestra próxima opción tiene 15 posibilidades, luego 14, 13, 12, 11, … etc. Y las permutaciones totales son:
16 × 15 × 14 × 13 × … = 20,922,789,888,000
Pero tal vez no queremos elegirlos a todos, solo 3 de ellos, y eso es entonces:
16 × 15 × 14 = 3,360
En otras palabras, hay 3,360 formas diferentes en que 3 bolas de billar podrían organizarse de 16 bolas.
Sin repetición, nuestras elecciones se reducen cada vez.
Pero, ¿cómo escribimos eso matemáticamente? Respuesta: utilizamos la función factorial [ “
 |
La función factorial (símbolo: ! ) solo significa multiplicar una serie de números naturales descendentes. Ejemplos:
|
| Nota: generalmente se acepta que 0! = 1 . Puede parecer gracioso que multiplicar ningún número juntos nos da 1, pero ayuda a simplificar muchas ecuaciones. | |
Entonces, cuando queremos seleccionar todas de las bolas de billar, las permutaciones son:
16! = 20,922,789,888,000
Pero cuando queremos seleccionar solo 3, no queremos multiplicar después de 14. ¿Cómo hacemos eso? Hay un buen truco: ¡dividimos por 13!
16 × 15 × 14 × 13 × 12 … 13 × 12 … [19459044 ] = 16 × 15 × 14
Eso estuvo bien. El 13 × 12 × … etc. se “cancela”, dejando solo 16 × 15 × 14 .
La fórmula está escrita:
|
n! (n – r)! |
| donde n es la cantidad de cosas para elegir, y elegimos r de ellos, sin repeticiones, el orden importa. |
Ejemplo Nuestro “ejemplo de orden de 3 de 16 bolas de billar” es:
| 16! | = | 16! | = | 20,922,789,888,000 | = 3,360 |
| (16-3)! | 13! | 6,227,020,800 |
(que es lo mismo que: 16 × 15 × 14 = 3,360 )
Ejemplo: ¿De cuántas maneras se puede otorgar el primer y segundo lugar a 10 personas?
| 10! | = | 10! | = | 3,628,800 | = 90 |
| (10-2)! | 8! | 40,320 |
(que es lo mismo que: 10 × 9 = 90 )
Notación
En lugar de escribir la fórmula completa, las personas usan diferentes anotaciones como estas:
Ejemplo: P (10,2) = 90
Combinaciones
También hay dos tipos de combinaciones (recuerde que el orden no importa ahora):
- Se permite la repetición : como monedas en el bolsillo (5,5,5,10,10)
- Sin repetición : como números de lotería (2,14,15,27,30,33)
1. Combinaciones con repetición
En realidad, estos son los más difíciles de explicar, por lo que volveremos a esto más adelante.
2. Combinaciones sin repetición
Así es como funcionan las loterías . Los números se sortean uno a la vez, y si tenemos los números de la suerte (sin importar el orden) ¡ganamos!
La forma más fácil de explicarlo es:
- suponga que el orden sí importa (es decir, permutaciones),
- luego modifíquelo para que el orden no importe.
Volviendo a nuestro ejemplo de bolas de billar, digamos que solo queremos saber qué 3 bolas de billar se eligen, no el orden.
Ya sabemos que 3 de cada 16 nos dieron 3.360 permutaciones.
¡Pero muchos de ellos son iguales para nosotros ahora, porque no nos importa el orden!
Por ejemplo, supongamos que se eligen las bolas 1, 2 y 3. Estas son las posibilidades:
| El orden sí importa | El orden no importa |
| 1 2 3 1 3 2 2 1 3 2 3 1 3 1 2 3 2 1 |
1 2 3 |
Entonces, las permutaciones tienen 6 veces más posibilidades.
De hecho, hay una manera fácil de determinar cuántas formas se pueden ordenar “1 2 3”, y ya hemos hablado de ello. La respuesta es:
3! = 3 × 2 × 1 = 6
(Otro ejemplo: 4 cosas se pueden colocar en 4! = 4 × 3 × 2 × 1 = 24 formas diferentes, ¡pruébelo usted mismo!)
Entonces ajustamos nuestra fórmula de permutaciones a y la reducimos de cuántas maneras podrían estar los objetos en orden (porque ya no estamos interesados en su orden):
Esa fórmula es tan importante que a menudo se escribe entre paréntesis grandes como este:
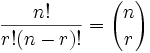 |
| donde n es la cantidad de cosas para elegir, y elegimos r de ellos, sin repetición, El orden no importa. |
A menudo se le llama “n elige r” (como “16 elige 3”)
Y también se conoce como el Coeficiente binomial .
Notación
Además de los “grandes paréntesis”, las personas también usan estas anotaciones:
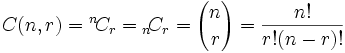
Solo recuerda la fórmula:
n! r! (N – r)!
Ejemplo: bolas de billar (sin orden)
Entonces, nuestro ejemplo de bola de billar (ahora sin orden) es:
16! 3! (16−3)! = 16! 3! × 13!
= 20,922,789,888,000 6 × 6,227,020,800
= 560
O podríamos hacerlo de esta manera:
16 × 15 × 14 3 × 2 × 1 = 3360 6 [ 19459044] = 560
Es interesante observar también cómo esta fórmula es agradable y simétrica :
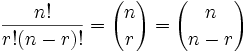
En otras palabras, elegir 3 bolas de 16, o elegir 13 bolas de 16 tienen el mismo número de combinaciones.
16! 3! (16−3)! = 16! 13! (16−13)! = 16! 3! × 13! = 560
Triángulo de Pascal
También podemos usar Triángulo de Pascal para encontrar los valores. Baje a la fila “n” (la fila superior es 0), y luego a lo largo de los lugares “r” y el valor allí es nuestra respuesta. Aquí hay un extracto que muestra la fila 16:
1 15 105 455 1365 …
1 16 120 560 1820 4368 …
1. Combinaciones con repetición
OK, ahora podemos abordar este …

Digamos que hay cinco sabores de helado: plátano, chocolate, limón, fresa y vainilla .
Podemos tener tres cucharadas. ¿Cuántas variaciones habrá?
Usemos letras para los sabores: {b, c, l, s, v}. Las selecciones de ejemplo incluyen
- {c, c, c} (3 cucharadas de chocolate)
- {b, l, v} (una de plátano, limón y vainilla)
- {b, v, v} (uno de plátano, dos de vainilla)
(Y para ser claros: hay n = 5 cosas para elegir, y elegimos r = 3 de ellas.
El orden no importa, ¡y nosotros podemos repetir!)
Ahora, no puedo describirte directamente cómo calcular esto, pero puedo mostrarte una técnica especial que te permite resolverlo.
Piensa en el helado que está en cajas, podríamos decir “pasa de la primera caja, luego toma 3 bolas, luego mueve 3 cajas más hasta el final” y ¡tendremos 3 bolas de chocolate!
Entonces, es como si estuviéramos ordenando a un robot que obtenga nuestro helado, pero no cambia nada, todavía obtenemos lo que queremos.
Podemos escribir esto como (flecha significa mover , círculo significa primicia ).
De hecho, los tres ejemplos anteriores se pueden escribir así:
| {c, c, c} (3 cucharadas de chocolate): | |
| {b, l, v} (una de plátano, limón y vainilla): | |
| {b, v, v} (uno de plátano, dos de vainilla): | |
OK, así que en lugar de preocuparnos por diferentes sabores, tenemos una pregunta más simple : “¿de cuántas maneras diferentes podemos organizar flechas y círculos?”
Tenga en cuenta que siempre hay 3 círculos (3 bolas de helado) y 4 flechas (necesitamos movernos 4 veces para pasar del 1er al 5to contenedor).
Entonces (siendo general aquí) hay r + (n − 1) posiciones, y queremos elegir r de ellos para tener círculos.
Esto es como decir “tenemos r + (n − 1) bolas de billar y queremos elegir r de ellas “. En otras palabras, ahora es como la pregunta de las bolas de billar, pero con números ligeramente cambiados. Y podemos escribirlo así:
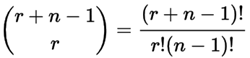 |
| donde n es la cantidad de cosas para elegir, y elegimos r de ellos repetición permitida, El orden no importa. |
Curiosamente, podemos mirar las flechas en lugar de los círculos y decir “tenemos r + (n − 1) posiciones y queremos elegir [19459006 ] (n − 1) de ellos tienen flechas “, y la respuesta es la misma:
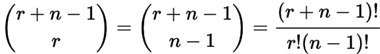
Entonces, ¿qué pasa con nuestro ejemplo, cuál es la respuesta?
| (3 + 5−1)! | = | 7! | = | 5040 | = 35 |
| 3! (5−1)! | 3! × 4! | 6 × 24 |
Hay 35 formas de tener 3 bolas de cinco sabores de helado.
En conclusión
Uf, eso fue mucho para absorber, así que tal vez podrías leerlo de nuevo para estar seguro.
Pero saber cómo funcionan estas fórmulas es solo la mitad de la batalla. Descubrir cómo interpretar una situación del mundo real puede ser bastante difícil.
Pero al menos ahora sabe cómo calcular las 4 variaciones de “El orden importa / no importa” y “Las repeticiones están / no están permitidas”.

