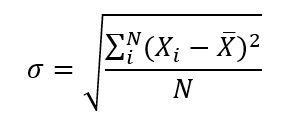
Fórmulas de desviación estándar
La desviación solo significa qué tan lejos de lo normal
Desviación estándar
La desviación estándar es una medida de cómo se extendió
nuestros números son .
Es posible que desee leer esta página más simple sobre Desviación estándar primero.
Pero aquí explicamos las fórmulas .
El símbolo de la desviación estándar es σ (la letra griega sigma).
Esta es la fórmula para la desviación estándar:
![square root of [ (1/N) times Sigma i=1 to N of (xi - mu)^2 ]](https://www.mathsisfun.com/data/images/standard-deviation-formula.gif)
¿Decir qué? ¡Por favor explique!
OK. Vamos a explicarlo paso a paso.
Digamos que tenemos un montón de números como 9, 2, 5, 4, 12, 7, 8, 11.
Para calcular la desviación estándar de esos números:
- 1. Calcule la media (el promedio simple
de los números) - 2. Luego, para cada número: reste la media y el cuadrado al resultado
- 3. Luego calcule la media de esas diferencias al cuadrado.
- 4. ¡Toma la raíz cuadrada de eso y listo!
La fórmula en realidad dice todo eso, y te mostraré cómo.
La fórmula explicada
Primero, tengamos algunos valores de ejemplo para trabajar:
Ejemplo: Sam tiene 20 Rosales.
El número de flores en cada arbusto es
9, 2, 5, 4, 12, 7, 8, 11, 9, 3, 7, 4, 12, 5, 4, 10, 9, 6, 9, 4
Calcule la desviación estándar.
Paso 1. Calcula la media
En la fórmula anterior μ (la letra griega “mu”) es la media de todos nuestros valores …
Ejemplo: 9, 2, 5, 4, 12, 7, 8, 11, 9, 3, 7, 4, 12, 5, 4, 10, 9, 6, 9, 4
La media es:
9 + 2 + 5 + 4 + 12 + 7 + 8 + 11 + 9 + 3 + 7 + 4 + 12 + 5 + 4 + 10 + 9 + 6 + 9 + 4
20
=
140
20
= 7
Entonces:
μ = 7
Paso 2. Luego, para cada número: restar la media y elevar al cuadrado el resultado
Esta es la parte de la fórmula que dice:
Entonces, ¿qué es x i ? Son los valores individuales de x 9, 2, 5, 4, 12, 7, etc.
En otras palabras x 1 = 9, x 2 = 2, x 3 = 5, etc.
Entonces dice “para cada valor, reste la media y cuadre el resultado”, así
Ejemplo (continuación):
(9 – 7) 2 = (2) 2 = 4
(2 – 7) 2 = (-5) 2 = 25
(5 – 7) 2 = (-2) 2 = 4
(4 – 7) 2 = (-3) 2 = 9
(12 – 7) 2 = (5) 2 = 25
(7 – 7) 2 = (0) 2 = 0
(8 – 7) 2 = (1) 2 = 1
… etc …
Y obtenemos estos resultados:
4, 25, 4, 9, 25, 0, 1, 16, 4, 16, 0, 9, 25, 4, 9, 9, 4, 1, 4, 9
Paso 3. Luego calcula la media de esas diferencias al cuadrado.
Para calcular la media, sume todos los valores y luego divida por cuántos .
Primero sume todos los valores del paso anterior.
Pero, ¿cómo decimos “sumarlos todos” en matemáticas? Utilizamos “Sigma”: Σ
El práctico Notación Sigma dice que resumir tantos términos como queramos:
Notación Sigma
Queremos sumar todos los valores de 1 a N, donde N = 20 en nuestro caso porque hay 20 valores:
Ejemplo (continuación):
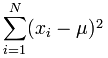
Lo que significa: Suma todos los valores de (x 1 -7) 2 a (x N -7) 2 [ 19459006]
Ya calculamos (x 1 -7) 2 = 4, etc. en el paso anterior, así que solo suma:
= 4 + 25 + 4 + 9 + 25 + 0 + 1 + 16 + 4 + 16 + 0 + 9 + 25 + 4 + 9 + 9 + 4 + 1 + 4 + 9 = 178 [19459010 ]
Pero esa no es la media todavía, necesitamos dividir por cuántos , lo que se hace por multiplicando por 1 / N (lo mismo que dividir por N):
Ejemplo (continuación):
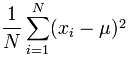
Media de las diferencias al cuadrado = (1/20) × 178 = 8.9
(Nota: este valor se llama “Varianza”)
Paso 4. Toma la raíz cuadrada de eso:
Ejemplo (concluido):
σ = √ (8,9) = 2.983 …
¡HECHO!
Desviación estándar de muestra
Pero espera, hay más …
… a veces nuestros datos son solo una muestra de toda la población.
Ejemplo: Sam tiene 20 rosales, ¡pero solo contó las flores en 6 de ellos !
La “población” son los 20 rosales,
y la “muestra” son los 6 arbustos de los que Sam contó las flores.
Digamos que los recuentos de flores de Sam son:
9, 2, 5, 4, 12, 7
Todavía podemos estimar la desviación estándar.
Pero cuando usamos la muestra como una estimación de toda la población , la fórmula de la Desviación Estándar cambia a esto:
La fórmula para Desviación estándar de muestra :
![square root of [ (1/(N-1)) times Sigma i=1 to N of (xi - xbar)^2 ]](https://www.mathsisfun.com/data/images/standard-deviation-sample.gif)
El cambio importante es “N-1” en lugar de “N” (que se llama “corrección de Bessel”).
Los símbolos también cambian para reflejar que estamos trabajando en una muestra en lugar de toda la población:
- La media es ahora x (para la media de la muestra) en lugar de μ (la media de la población),
- Y la respuesta es s (para Desviación estándar de muestra) en lugar de σ .
Pero eso no afecta los cálculos. Solo N-1 en lugar de N cambia los cálculos.
OK, calculemos ahora la Desviación estándar de muestra :
Paso 1. Calcula la media
Ejemplo 2: Uso de valores muestreados 9, 2, 5, 4, 12, 7
La media es (9 + 2 + 5 + 4 + 12 + 7) / 6 = 39/6 = 6.5
Entonces:
x = 6,5
Paso 2. Luego, para cada número: restar la media y elevar al cuadrado el resultado
Ejemplo 2 (continuación):
(9 – 6,5) 2 = (2,5) 2 = 6,25
(2 – 6.5) 2 = (-4.5) 2 = 20.25
(5 – 6.5) 2 = (-1.5) 2 = 2.25
(4 – 6,5) 2 = (-2,5) 2 = 6,25
(12 – 6,5) 2 = (5,5) 2 = 30,25
(7 – 6.5) 2 = (0.5) 2 = 0.25
Paso 3. Luego calcula la media de esas diferencias al cuadrado.
Para calcular la media, sume todos los valores y luego divida por cuántos .
Pero espere … estamos calculando la Muestra Desviación estándar, así que en lugar de dividir entre cuántos (N), dividiremos por N-1
Ejemplo 2 (continuación):
Suma = 6.25 + 20.25 + 2.25 + 6.25 + 30.25 + 0.25 = 65.5
Dividir entre N-1 : (1/5) × 65.5 = 13.1
(Este valor se denomina “Variación de muestra”)
Paso 4. Toma la raíz cuadrada de eso:
Ejemplo 2 (concluido):
s = √ (13.1) = 3.619 …
¡HECHO!
Comparación
Cuando utilizamos toda la población obtuvimos: Media = 7 , Desviación estándar = 2.983 …
Cuando usamos la muestra obtuvimos: Media de la muestra = 6.5 , Desviación estándar de la muestra = 3.619 …
Nuestra media muestral estaba equivocada en un 7%, y nuestra desviación estándar muestral estaba equivocada en un 21%.
¿Por qué tomar una muestra?
Principalmente porque es más fácil y más barato.
Imagina que quieres saber lo que piensa todo el país … no puedes preguntarle a millones de personas, así que en lugar de eso le preguntas a quizás 1,000 personas.
Hay una buena cita (posiblemente por Samuel Johnson):
“No es necesario comer todo el buey para saber que la carne es dura”.
Esta es la idea esencial del muestreo. Para encontrar información sobre la población (como la media y la desviación estándar), no necesitamos mirar a todos miembros de la población; solo necesitamos una muestra.
Pero cuando tomamos una muestra, perdemos algo de precisión.
Resumen
|
La Población Desviación estándar: |
|
|
| La Muestra Desviación estándar: | |